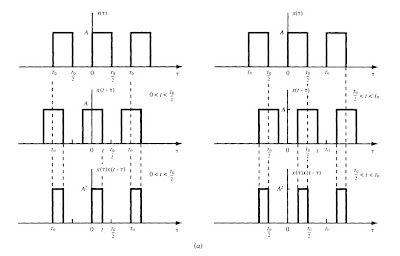
Two most important attributes of systems are linearity and time-invariance. We develop the fundamental input-output relationship for systems having these attributes. It will be shown that the input-output relationship for LTI systems is described in terms of a convolution operation. The importance of the convolution operation in LTI systems stems from the fact that knowledge of the response of an LTI system to the unit impulse input allows us to find its output to any input signals. Specifying the input-output relationships for LTI systems by differential and difference equations will also be discussed.

We give some examples about convolution integral in the post.

If you want to see them clearly, click the images. You can click right mouse button on images, click "save as" and download the image to your computer.

Devamını Oku...

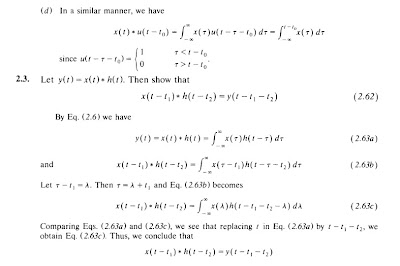
CONTINUOUS TIME LTI SYSTEMS: THE CONVOLUTION INTEGRAL

In analogy with the results derived and discussed in the preceding section, the goal of this section is to obtain a complete characterization of a continuous-time LTI system in terms of its unit impulse response. In discrete time, the key to our developing the convolution sum was the sifting property of the discrete-time unit impulse-that is, the mathematical representation of a signal as the superposition of scaled and shifted unit impulse functions. Intuitively, then, we can think of the discrete-time system as responding to a sequence of individual impulses. In continuous time, of course, we do not have a discrete sequence of input values. Nevertheless, as we discussed, if we think of the unit impulse as the idealization of a pulse which is so short that its duration is inconsequential for any real, physical system, we can develop a representation for arbitrary continuous-time signals in terms of these idealized pulses with vanishingly small duration, or equivalently, impulses. This representation is developed in the next subsection, and, following thet, we will proceed very much as to develop the convolution integral representation for continuous-time LTl systems.

If you want to see them clearly, click the images. You can click right mouse button on images, click "save as" and download the images to your computer.

Devamını Oku...