The Convolution Sum: Discrete-Time LTI Systems

INTRODUCTION

We introduced and discussed a number of basic system properties. Two of these, linearity and time invariance, play a fundamental role in signal and system analysis for two major reasons. First, many physical processes possess these properties and thus can be modeled as linear time-invariant (LTI) systems. In addition. LTI systems can be analyzed in considerable detail, providing both insight into their properties and a set of powerful tools that form the core of signal and system analysis.

In this chapter, we begin the development by deriving and examining a fundamental and extremely useful representation for LT1 systems and by introducing an important class of these systems.

One of the primary reasons LTI systems are amenable to analysis is that any such system possesses the superposition property described. As a consequence, if we can represent the input to an LTI system in terms of a linear combination of a set of basic signals, we can then use superposition to compute the output of the system in terms of its responses to these basic signals.

As we will see in the following sections, one of the important characteristics of the unit impulse, both in discrete time and in continuous time, is that very general signals can be represented as linear combinations of delayed impulses. This fact, together with the properties of superposition and time invariance, will allow us to develop a complete characterization of any LTI system in terms of its response to a unit impulse. Such a representation, referred to as the convolution sum in the discrete-time case and the convoluiton integral in continuous time, provides considerable analytical convenience in dealing with LTI systems- Following our development of the convolution sum and the convolution integral we use these characterizations to examine some of the other properties of LTI systems. We then consider the class of continuous-time systems described by linear constantcoefficient differential equations and its discrete-time counterpart, the class of systems described by linear constant-coefficient difference equations. We will return to examine these two very important classes of systems on a number of occasions in subsequent chapters. Finally, we will take another look at the continuous-time unit impulse function and a number of other signals that are closely related to it in order to provide some additional insight into these idealized signals and, in particular, to their use and interpretation in the context of analyzing LTl systems.

DISCRETE-TIME LTI SYSTEMS: THE CONVOLUTION SUM

The Representation of Discrete-Tme Signals in Terns of Impulses

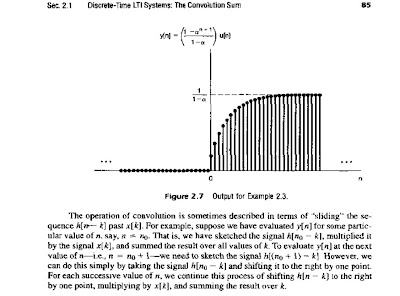
The key idea in visualizing how the discrete-time unit impulse can be used to construct any discrete-time signal is to think ofa discrete-time signal as a sequence of individual impulses. To see how this intuitive picture can be turned into a mathematical representation.

If you want to see them clearly, click the images. You can click right mouse button on images, click "save as" and download the image to your computer.